<기초 통계기법 활용>
1. 평균: 분포가 대칭일 때 데이터 집합의 중앙이 어딘지 알 수 있는 지표. (데이터의 합)/개수
2. 중앙값: 크기에 따라 차례로 나열했을 때 가운데 값. n이 홀수면 (n+1)/2번째 값
평균에 비해 이상치에 의한 영향을 덜 받으며 데이터 분포가 비대칭일 때 평균보다 유의미
3. 최빈치: 데이터 집합에서 가장 많은 빈도를 갖는 값. 중앙값이랑 같은 속성!
4. 분산: 평균으로부터 각각의 데이터가 얼마나 떨어져 있는지를 종합적으로 나타내는 지표.
=(각 데이터 – 평균)^2의 합/(n-1) R에서 var() 함수 써서 구함
평균이 포함되어있고 제곱해서 이상치 매우 민감. 본래 데이터의 속성값과도 다른 단위
5. 표준편차: 분산의 단위를 본래의 척도와 맞춰주기 위해 분산을 제곱근한 것(루트씌운)
R에서 sqrt() 함수 써서 구함
6. 범위 Range: 데이터 집합의 확산 정도를 R=(최대값-최소값)으로 나타낸 것.
히스토그램: 속성의 범주를 수 개의 영역으로 나누고 각 영역에 해당하는 막대그래프를 생성함
상자 그림: 최대/최소/중앙/사분편차를 사용하여 극단값이 어떤지를 보게 함. 이상치는 따로 표시
<데이터 분석 기법: 상관분석, 회귀분석, 주성분분석>
[상관분석 기법]
두 변수 간의 선형적인 관계를 정량적인 지표로 나타낸 것.
두 변수 x1, x2 간의 상관 정도를 나타내는 공분산을 이용한다. 공분산=0이면 관계없음을 의미

x1i=x1의 i번째 관측치
x1바=x1의 표본평균
상관계수: 두 모집단을 나타내는 변수 x1, x2간의 선형관계를 나타내는 척도 p
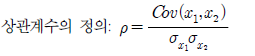
Cov()= 두 모집단의 공분산
분모 애들은 x1, x2의 표준편차
표본 상관계수 = 피어슨 상관계수r

-1<=r<=1
r=0이면 변수 간 상관관계 없음
r의 절대값이 클수록 상관성 높음=유의성 높음
[회귀분석 기법]
회귀분석은 한 변수가 다른 변수에 미치는 영향을 함수 형태로 추정하기 위한 기법.
독립변수 x1, x2, …, xn과 종속변수 y에 대해 다음의 회귀분석 모형들이 존재한다.
독립변수들에 대한 분산분석결과 p-value>0.05인 변수들은 종속변수에 유의한 것으로 판정.
1. 단순회귀분석: 독립변수 1개. 종속변수와의 관계가 선형적(1차 함수)

알려지지 않은 모수를 근사화하기 위해 오차를 최소로 하는 최소제곱법 사용, 모수들 추정
2. 다중회귀분석: 독립변수 2개 이상. 종속변수와의 관계가 선형적(1차 함수)

3. 곡선회귀분석: 독립변수 1개. 종속변수와의 관계가 곡선적(2차 함수 이상)

[주성분 분석]
n개의 변수들을 선형 결합하여 더 적은 개수의 변수들로 데이터를 표현(=차원 축소)하고, 이를 이용하여 데이터를 분석하기 위해 사용되는 기법
분산의 크기에 따라 제 k주성분이라고 표시된 선을 새 좌표축으로 하여 데이터를 투영시킴.
1. 제1 주성분 계산: 데이터 집합 x1...xn을 나타내는 x의 제1 주성분 w1은

2. 제k 주성분 계산: k번째 주성분 wk을 구하기 위해 k-1개의 주성분을 데이터 집합에서 빼줌

'데이터베이스 DB' 카테고리의 다른 글
| 데이터 오류 종류 (0) | 2020.08.16 |
|---|---|
| 데이터 분석 모형 검증: 탐색적 분석 (0) | 2020.08.16 |
| 분석용 데이터 탐색 101: 기본 용어, 표본 추출 기법, 척도 종류(질적/양적 속성) (0) | 2020.08.16 |
| tidyr 패키지가 하는 일, 함수들 (0) | 2020.03.20 |
| dplyr 패키지 용도, 각 함수가 하는 일 (0) | 2020.03.20 |


댓글